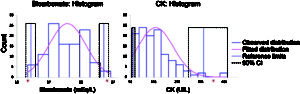
Frequency distribution curve (counts versus test result) of bicarbonate and creatine kinase (CK) results obtained from 124 dogs as part of a reference interval determination study at Cornell University. Bicarbonate results from the dogs show a symmetrical distribution around the mean value, indicating that parametric statistical methods can be used to establish the interval, i.e. mean+/-2SD. The vertical blue lines at either end of both graphs indicate the determined upper and lower reference limits for that analyte. The dashed box around each of the limits represents the 90% confidence interval on the limit (which is really just a statistical estimate). Note, how results from some of the healthy dogs fall outside (above or below) the reference interval (red asterixes in both graphs) and that some of the results are even beyond the 90% CI of the upper limit for bicarbonate and CK. This indicates that results above or below a reference interval may not be abnormal (but still could be). In contrast to bicarbonate, the results for CK are clearly skewed to the left, with more dogs having lower than higher CK activity. Parametric statistical methods could not be used for establishing an interval for CK, unless the distribution became normal on log transformation (it did not). Therefore, non-parametric statistical methods or percentiles should be used for establishing the reference interval for CK. If you look carefully at the CK data, one or two dogs have values far beyond the rest of the dogs (451 U/L versus next highest at 351 U/L). The results for these two dogs was outside the upper reference limit (they would have been flagged as “high”) but within the 90% confidence interval for that upper limit. The program (and your eye) did identify these results as outliers. Do you exclude them or not from the reference interval determination (since they were “excluded” anyhow)? Only if you have a valid reason. Inclusion of such identified outliers will broaden your interval at the risk of decreasing sensitivity (ability to detect an abnormal result) for the sake of specificity (fewer false positive results). Excluding these outliers will narrow the reference interval, which will have the opposite effect: maximizing sensitivity at the expense of specificity (may get more false positive results). In the case of CK, the higher CK activity in the two dogs was attributed to a collection artifact (from a muscle stick during venipuncture) and the results were excluded (these two dogs also had higher AST activity than the other dogs, helping to justify their exclusion). If a valid reason to exclude the outliers was not identified, ideally they should be left in as long as the reference interval is so broad that it becomes useless (this is the judgement of the clinical pathologist overseeing the reference interval determination).